《用字母表示数》课堂实录（续）

天水市逸夫实验中学  高旭宇

步骤三：多媒体展示：你能用字母a，b表示正方形的面积吗？（如图）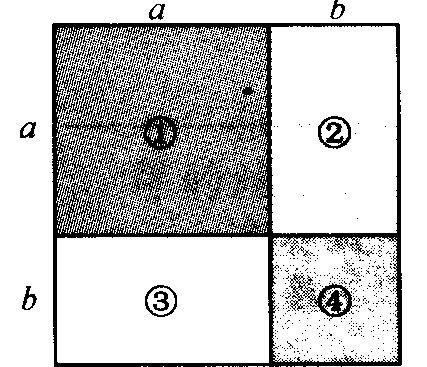

生5：(a+b)(a+b)或(a+b)²

生6：可以分成四部分计算，即：a²+b²+ab+ab。

生7：还可以看成两个长方形计算，即：a(a+b)+b(a+b) 。

生8（猛地站起身）：还可以看成竖放的两个长方形……（又不好意思的坐下）：嘿嘿，和前面同学的结果一样…（学生笑）。

生9：其实a²+b²+ab+ab和a(a+b)+b(a+b)也一样。    师：是吗？      生：是，去括号就一样了。

师：非常好！实际上这三个式子只是形式不同，本质都是正方形的面积，即：(a+b)²= a²+b²+ab+ab =a(a+b)+b(a+b)。可见用字母可以把一个图形的面积用多种方法表示，真神奇！

（此时同学们热情高涨，兴趣盎然，为突破难点奠定了情感基础。）

步骤四：用字母表示数还可以使一些复杂问题变简单！

多媒体展示：你能把每一个图中阴影部分的小正方形个数对应地用一个含字母的式子表示吗？

生10：后一个图中阴影正方形个数是前一个的二倍，如果图（1）阴影部分用a表示，图（2）就是2a，图（3）就是4a……

学生一起纠正：图（3）是10个，不是图（2）6个的二倍！图（4）是15个，也不是图（3）的二倍（生10不好意思的坐下）。

师：至少他发现了图（1）、图（2）的关系，继续努力！

生11：设每个图中正方形的总数为a，则阴影部分正方形个数为 a。      生齐：对！

师：这是个有创造性的思路！

生12：图（1）可表示为1+2，图（2）1+2+3……直到1+2+3+…+n。

师：n代表什么？

生：第n个图中大长方形的宽.

师：了不起！字母还可以这样来表示数!

生13：图（1）还可表示为 。

师（惊讶的）：2×3？这是什么意思？

生：网格的长×宽，再除以2就是阴影小正方形的个数。其实我是受到了生11的启发才想到的。

师（板书）：1+2= 。太好了！前三位同学的发现结合得到了一个等式！

同学们（沉默片刻）：对呀！每个图都能这样表示！

生14（激动地）：图（2）可表示为1+2+3= ！

学生齐答：图（3）可表示为1+2+3+4= ！     图（4）可表示为1+2+3+4+5= ！……

教师微笑着一一板书。

师：那么，如果是n×(n+1)这样的正方形网格呢？

生15：可表示为1+2+3+…+n=

师：你比数学家高斯更聪明，因为字母n可以表示任何正整数！如第200个图中阴影正方形的个数怎么表示？

生16：1+2+3+…+200= =20100。      师：第2000个图能算吗？       生：能！ 

师：我们的成收获实在太大了！我们得到了自然数的求和公式，也叫高斯求和。而且更奇妙的是，这个公式竟然可以用前面的图形画出来！

   （在此过程中，更应注重的是学生从事探索性活动的投入程度和积极性，而不完全是学生得到的答案。）

例1：填空

（1）一打铅笔有12枝，n打铅笔有        枝；

（2）三角形的三边长分别为3a，4a，5a，则其周长为           ；

（3）如图5，某广场四角铺上了四分之一圆形的草地，若圆形的半径为r米，则共有草地        平方米。

（4）我们知道      23=2×10+3；      865=8×10²+6×10+5；

类似地，5984=     ×10³+     ×10²+     ×10+     。

若某三位数的个位数字为a，十位数字为b，百位数字为c，则此三位数可表示为       。

师（小结）：字母表示数使一些数字规律更简明，更有普通性，为我们解决数字问题带来方便。今后，我们一起探索更多的更有趣的数学规律，好不好？     

生：好！       师：下课！

【教后记】

教师的工作决不能仅限于教给学生知识，更重要的要给学生打开一扇窗，让学生看到外面更大，也许是更美，也许是更复杂的世界。

本节课的设计也在试图为刚刚步入中学的“准中学生”们打开一扇通往“代数”这个奇妙世界的窗。面对学生如此积极的探索热情，一切的“标准答案”都已不在重要！

如果学生们只是站在远处眺望着数学说：“我不喜欢（甚至讨厌）数学”，那是多么悲哀的事情。（完）